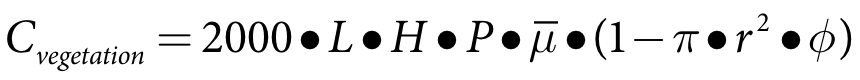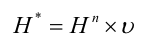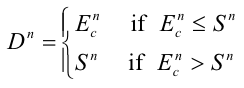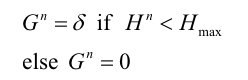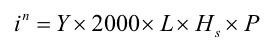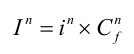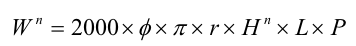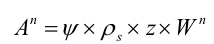Note: This is documentation for version 5.0 of Source. For a different version of Source, select the relevant space by using the Spaces menu in the toolbar above
RPM - Riparian Particulate Model for Riparian Buffers - SRG
The riparian particulate model (RPM) is used to model the trapping of sediment particles in riparian buffers and so reduce the load of sediment and associated constituents to streams. It is intended principally for catchment-scale applications.
Scale
The RPM model operates at the scale of a functional unit and at a daily time-step.
Principal developer
eWater is the principal developer building on work from the Cooperative Research Centre for Catchment Hydrology and CSIRO.
Scientific Provenance
Extensive work on controlling sediment and nutrient movement within catchments was undertaken by the CRC for Catchment Hydrology as summarised by Hairsine et al., (1997). This and other work was used create a conceptual model of particulate trapping in riparian buffers (Newham et al., 2005) which lead to the development of RPM as a plugin model in E2 and then WaterCAST (Argent, et al., 2008).
Version
Source version 4.5
Dependencies
The model requires functional units and sub-catchments/catchments. Runoff in terms of quick flow and slow flow must be available to the RPM model at a daily time-step. Sediment inputs to RPM must also be provided by Source.
Constraints and applicability
The application potential of the RPM is broad - the relatively simple conceptualisation enables the RPM to be applied at catchment scales across a wide range of physical environments. All the parameters of the model are measurable. However, the model currently relies upon the user to obtain site-specific information for several key model parameters. This might require the user to re-analyse existing data, and/or conduct site measurements.
The RPM is dependent on an accurate representation of a catchment’s hydrology for achieving adequate predictions of trapping efficiency. One especially important aspect is the accurate estimation of surface runoff. Estimates of ‘quick flow’ and ‘slow flow’ are available from Source runoff generation component models and RPM has a parameter to convert a proportion of ‘quick flow’ to surface runoff.
Flow phase
Riparian buffers are vegetated strips of land separating runoff and pollutant contributing areas from surface waters (Mickelson et al. 2003; Parkyn 2004). Riparian buffers play an important role in reducing pollutant inputs to streams; creating in-stream habitat and improving local landscape aesthetics (Karssies and Prosser 1999; Parkyn 2004).
Overland flow carries sediment and associated pollutants which are typically highly intermittent and spatially heterogeneous. Riparian buffers can be placed in a flow path and can act to change the overland flow by:
- Creating a physical barrier to slow the overland flow and promote particulate deposition;
- Spreading concentrated overland flow so that the slowing of overland flow is enhanced; and
- Infiltrating a portion of the overland flow into storage within the buffer - an effect enhanced by soil macropores frequently found in riparian buffers, and negated by zones of soil saturation that are frequently found in convergent parts of the landscape.
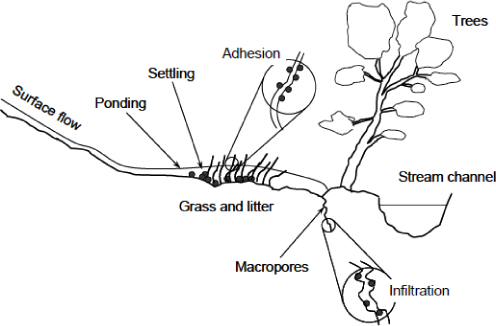
The performance of riparian buffers is governed by complex mechanisms (Muñoz-Carpena et al. 1999). During a surface flow event particulate matter from the hill slope is carried into the riparian buffer. The incoming particulate load comprises different size fractions and material of different chemical composition. Particle size distribution and chemical composition affect the proportion of material trapped, its behaviour in the riparian buffer (eg. re-entrainment, breakdown, release of solutes etc.), and its potential impact on the receiving stream. Figure 1 shows the three main processes that operate to trap particulates in a riparian buffer: settling, infiltration and adhesion.
Figure 1. Processes that remove particulates from surface flow in a riparian buffer: settling, adhesion and infiltration (Newham et al, 2005)
Model description
The Riparian Particulate Model (RPM) quantifies the particulate trapping capacity of riparian buffers through simulation of the processes of:
- settling
- infiltration
- adhesion.
RPM subdivides the total particulate load into two size classes:
- coarse - which is trapped principally by settling; and
- fine - which is trapped by infiltration and adhesion.
The RPM uses simplified descriptions of these three trapping mechanisms. It captures important features of experimental findings. RPM can be used to investigate the likely effects of changes to a range of important buffer characteristics to aid design of riparian buffers.
Settling
Overland flow during major runoff events can carry significant concentrations of coarse particulates that have moderate-high settling velocities in tranquil flow. Many such particles are chemically inert but have the potential to bury vegetation in the riparian zone and smother aquatic habitat.
Coarse particulates typically include fine gravels (>1000 μm), coarse sands (500-1000 μm), medium sands 250-500 μm), fine sands (100-250 μm) and very fine sands (50-100 μm). The coarse fraction also includes some organics (eg, detritus such as twigs and grass stems, organic soil particles etc.) and some contaminants (eg, nutrients, heavy metals, pathogens etc.) which may adhere to such particles. With knowledge of the systems being modelled, RPM users can specify the proportion of the coarse and fine particulates. Management of coarse particulates usually focuses upon increasing friction, reducing flow velocities, encouraging ponding and settling, and combating channelisation.
Where surface flow velocity falls, water depth increases and particles have the opportunity to settle. Groundcover (typically grass) and coarse litter (branches, sticks, twigs etc.) in a riparian buffer increase friction, cause water to pond and hence accelerate the settling process. This is most effective when surface flow is distributed evenly across the land surface (viz., sheet flow). Channelisation of flow maintains high velocity, reduces settling and is a major impediment to particulate trapping because it causes flow to by-pass the main trapping zones. Flow may become channelised naturally through scouring along the main flow path, and may be exacerbated by animal and farm tracks and roads (Hairsine et al. 2001). At a smaller scale, flow often becomes channelised around clumps of vegetation, large woody debris and other obstacles in the buffer.
Groundcover (eg, grass) provides a matrix of stems that increase friction, increase water depth, reduce velocity and hence decrease the capacity of the flow to transport particulates. Riparian buffers perform best when they comprise a dense vegetative cover of sufficient height and stiffness to avoid inundation during large runoff events (Collier et al. 1995).
Infiltration and adhesion
Fine particulates are more difficult to trap than coarse particulates - their settling velocities are very low, and they are generally more easily eroded and transported. Fine particulates include clays (<2 μm), silts (2-20 μm) and may include very fine sands (50-100 μm). Fine particulates often carry a disproportionately large percentage of the total load of contaminants (eg. nutrients, pathogens, heavy metals, pesticides etc.) because of their high surface area to volume ratio (Flood and Ashbolt 1999).
Where fine particulates pose a threat to receiving water quality, management of the riparian buffer needs to focus upon infiltration and adhesion as trapping mechanisms; water that infiltrates into riparian soils leaves behind almost all its particulate load. Only extremely small particles pass through macropores (sub-surface flow creation and drainage pathways created by soil cracking, plant root growth and decay, burrowing creatures and soil fauna). Maintaining infiltration rates at high levels can be achieved by minimising soil compaction (eg, excluding stock or grazing for short periods when soils are least likely to experience compaction), and increasing macropore volume.
Riparian groundcover and litter are often observed to be coated with fine sediment following inundation. Although the total mass of particulates trapped by adhesion is small, this removal process may be very important in reducing fine particulates loads.
Buffer performance
There are two processes that cause the performance of riparian buffers to decline over time. First, large events may bury vegetation, scour litter and/or clog macropores, thereby temporarily reducing the ability of the buffer to trap particulates during subsequent events. Trapping efficiency eventually recovers (eg. by grass growth through recently deposited particulates, litter accumulation and macropore re-establishment) but this may take weeks or months. Second, although buffers may trap organic particulates, these subsequently break down and may release significant quantities of soluble nutrient. For example, in a study of a small (6 km2) agricultural catchment in Western Australia, the establishment of riparian buffers had limited impact on measured TP concentrations or loads. The mineralisation of organic particulates was thought to have contributed to the observed shift from particulate to soluble phosphorus export (McKergow et al. 2003). The recovery of a buffer is simulated in the RPM but mineralisation processes are not.
Model structure
The RPM consists of three components which simulate particulate trapping:
- coarse particulates by settling;
- fine particulates by adhesion; and
- fine particulates by infiltration.
Figure 2 shows the structure of the RPM. Coarse particulate inputs are assumed to be trapped only by settling, and not by adhesion or infiltration. Fine particulate inputs can be trapped by adhesion or infiltration. The model user can adjust the definition of coarse and fine particulates to suit the problem being addressed and the available data. Details of the RPM model are provided in Newham et al. (2005) and summarised below.
Figure 2. Structure of RPM
Settling of coarse particulates
The volume within the grass part of the buffer that is available to trap sediment is:
| Equation 1 |
|---|
where:
Cvegetation void volume of the vegetation (m3);
H vertical effective vegetation height (m);
L buffer length (km);
P buffer width (flow path length) (m);
r average stem radius of the vegetation (m),
Φ average stem density (stems m-2);
µ the mean of cos(θ) for the buffer; and
θ buffer slope.
The factor of 2000 accounts for the fact that L has units of km and there are buffers on both sides of the stream. If water backs up to a height H up-slope from the buffer, then there is an additional volume of water in which sediment can settle:
Equation 2 |
|---|
where:
Cbackwater volume of backwater (m3).
When the slope is very small the term H/tan(θ), which is the distance the backwater extends upslope, is large. The additional volume is restricted to:
Equation 3 |
|---|
Equation 3 assumes that water backs up to effective vegetation height which may be an overestimate when the stem density is low.
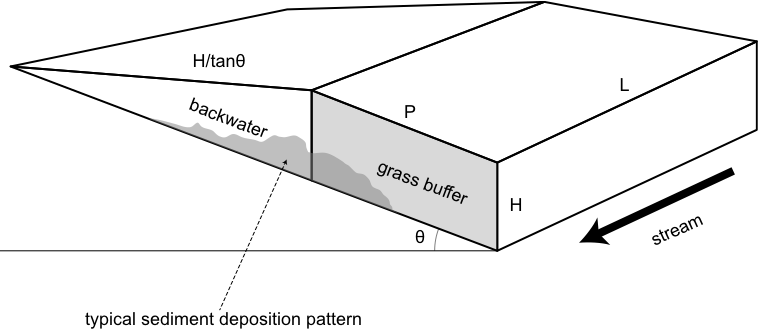
Most experimental studies find that flow path length, P is a significant factor in determining particulate trapping efficiency (Mickelson et al. 2003). Hook (2003) found that under conditions of relatively shallow flow, not concentrated in channels, gently sloping and densely-vegetated buffers were effective in limiting the transport of particulates from uplands to streams. However, narrow, moderately steep, sparsely vegetated buffers were vulnerable to much higher rates of particulate delivery. Rose et al. (2002; 2003) found that much of the coarse particulate material trapped by a grass buffer was deposited upslope from where the tall grass started. The reason is that high friction in the grass buffer slows the overland flow and causes a ‘backwater’ effect upslope from the grass (see Figure 3) where the water deepens, slows, the ‘carrying capacity’ decreases and sediment deposits. In the RPM we do not model the settling process explicitly in either the backwater or the vegetation. However, Equation 1 and Equation 3 quantify the maximum capacity of the buffer to trap particulates. Whether the buffer actually traps the volume of sediment suggested by Equation 1 and Equation 2 depends on the size of the runoff event, as discussed below.
Figure 3. Riparian grass buffer
Damage of vegetation during a runoff event is also a determinant of coarse particulate trapping. In a small runoff event the velocity through the buffer will be only moderate, the drag forces on the vegetation small and it is likely to remain erect and suffer little damage. We can expect that the majority of particulates delivered to the buffer will be trapped in such events. In a very large event, however, the velocity and depth of water in the buffer may be large, the drag and scour forces on the vegetation and soil will be high, and there may be substantial damage to vegetation. Even if permanent damage is low, stems will be bent over by the flow where they are more likely to be buried. Both processes lead to a reduction in the trapping capacity of the buffer. Thus in large events the trapping capacity is reduced, and in very large events trapping may be small.
The final factor considered is how quickly vegetation (and hence trapping capacity) recovers after a runoff event. If grass cover is sparse because of burial during a recent event, drought, shade or winter die-back then trapping efficiency may be low (Magette et al. 1989; Dillaha et al. 1989).
Effective vegetation height
The effective vegetation height is an estimate of the maximum depth of particulates that the riparian vegetation can trap before its performance as a filter declines significantly. In the case of stubble or mown grass it is closely approximated by the average stem length. In the case of long grass that is easily bent over by runoff, it is significantly less than the total stem length but can be approximated by the height of the grass sward after it has been pushed over (eg. by hand). Typically the effective vegetation height for lush grass will be 10-50 mm. For other groundcover the effective vegetation height may be greater (eg. sugar cane stubble) or smaller (eg. sparse or new grass). The effective vegetation height is a parameter that is best estimated from local knowledge of the types of groundcover found in the riparian buffer. It is easily measured during field visits.
Figure 4. Structure of the coarse particulate settling module of the RPM
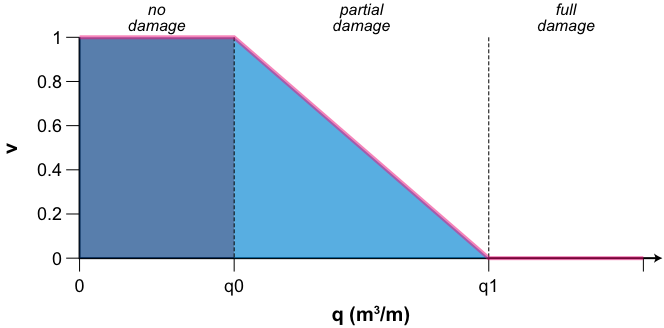
If the effective vegetation height on day n prior to a runoff event occurring is Hn then this value may be reduced during the event by the grass being flattened, damaged or buried. We assume there is a lower threshold of inflow per unit width of buffer q below which such effects are negligible qo, and an upper threshold q1 above which these effects are so severe that particulate trapping is reduced to zero (see Figure 5).
Figure 5. flow-dependent vegetation damage factor
The effective trapping height during an event is then:
| Equation 4 |
|---|
where:
Hn vegetation height on day n prior to the runoff event (m);
H* effective trapping height on day n during the runoff event (m)
ν flow-dependent vegetation damage factor on day n (dimensionless)
We assume a linear relationship for vegetation damage factor versus inflow per unit width:
Equation 5 |
|---|
where:
qn daily total flow per unit length of buffer on day n (m3 m-1)
qo daily total flow per unit length at which riparian vegetation beings to be damaged, reducing its effectiveness for particulate trapping (m3 m-1)
q1 daily total flow per unit length at which the riparian buffer is totally ineffective (m3 m-1).
The flow thresholds q0 and q1 for vegetation damage will vary depending upon the type and condition of groundcover in the riparian buffer (eg. mown grass, stubble, rank vegetation etc.). It will also depend upon the buffer slope and possibly the slope length of the sub-catchment. These thresholds are best estimated by the model user based on local knowledge.
Having accounted for damage, flattening or burial of vegetation (hereafter termed damage), the actual trapping capacity during the event is:
Equation 6 |
|---|
where:
Sn maximum amount of particulate material that can be trapped during day n (t)
L length of streams with riparian buffers on both banks (km)
P path length across the buffer (m)
ρ particulate density (t m-3)
The factor of 2000 accounts for the fact that L has units km and that streams have riparian buffers on both banks. Assuming that there is no additional restriction on particulate trapping, the buffer will trap the amount:
Equation 7 |
|---|
where:
Dn dialy total coarse particulate trapped on day n (t);
Enc daily total mass inflow of coarse particulates (t)
Sn trapping capacity on day n after correcting for vegetation damage (t)
The RPM assumes that the only effect of a large event is to reduce the trapping capacity of the vegetation and that high velocity and low residence time do not reduce settling, cause re-suspension or prevent particulates completely occupying the adjusted trapping capacity. This assumption is more realistic for medium-coarse sands than for fine sands and coarse silts. The user can define the boundary between coarse and fine particulates as they see fit. Although commonly the cut-off is set at 50 μm, it could be set at 100 or 200 μm provided the user specifies a coarse particulate generation model and input data consistent with this size definition (Rose et al. 2003).
At the end of the event on day n the vegetation height is re-calculated accounting for the amount of particulates deposited during the event and the amount of re-growth.
Equation 8 |
|---|
where:
Hn+1 effective vegetation height on day n + 1
Gn vegetation growth during day n (m)
| Equation 9 |
|---|
where:
δ daily vegetation growth rate (m)
Hmax maximum effective vegetation height (m).
To a first approximation the daily vegetation growth rate δ can be assumed constant. Growth rates need to be estimated from locally derived data on the relevant riparian.
Infiltration of fine particles
One important feature of riparian buffers is that soil compaction is reduced (by excluding stock) and permeability increases (by bioturbation and root growth/decay). As a result some fraction of the overland flow entering a riparian buffer zone infiltrates into the ground and its particulate load is trapped. In the RPM an approximate model is used to estimate the volume of water that infiltrates.
| Equation 10 |
|---|
where:
Y effective macroporosity (m3 m-3)
Hs depth of unsaturated porous soil layer (m)
The value of Hs is best estimated from locally derived soils information and a conservative estimate is the depth of the A-horizon. In the riparian zone, the water table often lies close to the surface and this may restrict the volume of water that can infiltrate. The water table depth can be approximated by the bank height. We recommend that Hs be estimated as the smaller of the bank height or depth to the A-soil horizon.
The mass of fine particulates trapped by infiltration is:
| Equation 11 |
|---|
where:
In daily total mass of fine particulates trapped on day n by infiltration (t)
in daily total volume of water that infiltrates on day n (m3)
Cnf concentration of fine particulates in surface runoff flowing into the buffer on day n (t m-3)
Infiltration may also contribute to the trapping of coarse particulates. However, it would be incorrect to use Equation 11 and simply replace Cnf, the concentration of fine particulates, by Cnc the concentration of coarse particulates flowing into the buffer in surface runoff on day n (t m-3). Settling in the riparian buffer will reduce the concentration so that Cnc will overestimate the mean concentration of coarse particulates, leading to Equation 11 overestimating the mass of coarse particulates trapped by infiltration. This is not the case for fine particulates whose settling velocity is low. In addition the mass of coarse particulates trapped by infiltration is expected to be small compared with the mass trapped by settling. For these reasons the RPM model neglects infiltration as a trapping mechanism for coarse particulates. We assume that the infiltration rate is independent of event size and remains constant over time (viz., there is no clogging of the macropores by fine particulates).
Adhesion of fine particulates
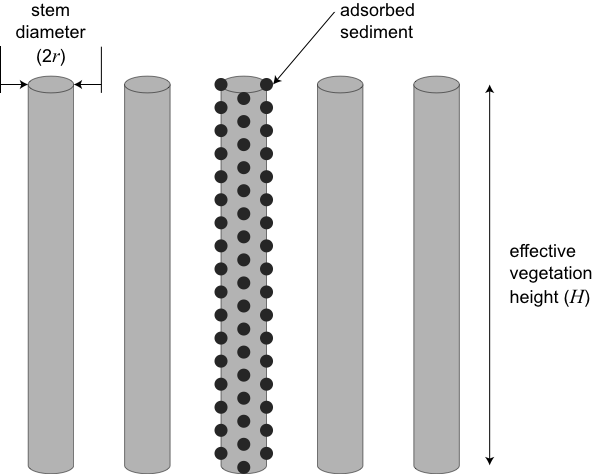
The trapping of fine particulates by adhesion to riparian vegetation is modelled in the RPM as a function of the available vegetative surface area and the thickness of the adsorbed layer (see Figure 1). Assuming that vegetation is approximately cylindrical then the total surface area of vegetation can be approximated by:
Equation 12 |
|---|
where:
Wn total surface area of vegetation per unit surface area of buffer (m2 m-2)
ø stem density (stems m-2)
r average stem radius (m)
Hn average stem height on day n (m)
L buffer length (km)
P buffer width (m).
If fine particulates are adsorbed uniformly over the surface area of the vegetation to a thickness z then the total mass of fine particulates adsorbed is:
Equation 13 |
|---|
where:
An daily total mass of fine particulates absorbed on day n (t)
z the average thickness of absorbed fine particulates (m)
ρs density of fine particulates (t m-3)
ψ packing factor (0 < ψ < 1). The packing factor accounts for the fact that sediment particles (here approximated as spheres) adhere to a surface so that they are touching each other, leaving void spaces in the sediment layer.
Figure 6. Flow dependent vegetation damage factor
It is difficult to estimate the likely thickness z and packing factor ψ of the adhesion layer a priori. It is tempting to postulate that only a single layer of fine particulates will stick to vegetation and detritus, and that the packing factor will be ~0.5. However, clay and other fine particles have a tendency to flocculate and form larger particles especially when there is a change in the ionic composition of water (eg. an increase in salinity). This could result in deposits several particle diameters thick. Another complication is that deposition may not be uniform because high shear stresses on some parts of the vegetation may remove deposited material, or prevent it from becoming adsorbed. The ideal approach is to conduct in situ experiments after an inundation event and estimate either the average deposit thickness or the mass deposited. In the absence of such data, the model user should run simulations with a range of plausible deposition thicknesses to determine the potential impact of adhesion on fine particulate fluxes. If the results are encouraging, further field investigations may be warranted to confirm the preliminary model predictions. There is no information available on how event size affects adhesion. The RPM assumes that Equation 13 holds regardless of event size. There is also no information available on how quickly adhesion sites filled during an event become available to adsorb fine particulates in a subsequent event. Currently, the RPM resets the adhesion capacity if there is one day or more without a surface runoff event.
Input data
Although the RPM model has simplified the process of modelling riparian buffer trapping mechanisms, the model still has considerable data requirements.
RPM relies on other component models in Source to provide a time series of quick flow that RPM converts to overland flow. RPM also accepts sediment input from other component models.
Input data on soil and vegetation characteristics are required (refer to Table 1).
Three physical riparian buffer parameters are required:
- the width of riparian vegetation - classified into a maximum of four classes
- the percentage length of each riparian buffer width class, as a percent of the total length of a river reach within a sub-catchment
- and the average slope of each buffer width class
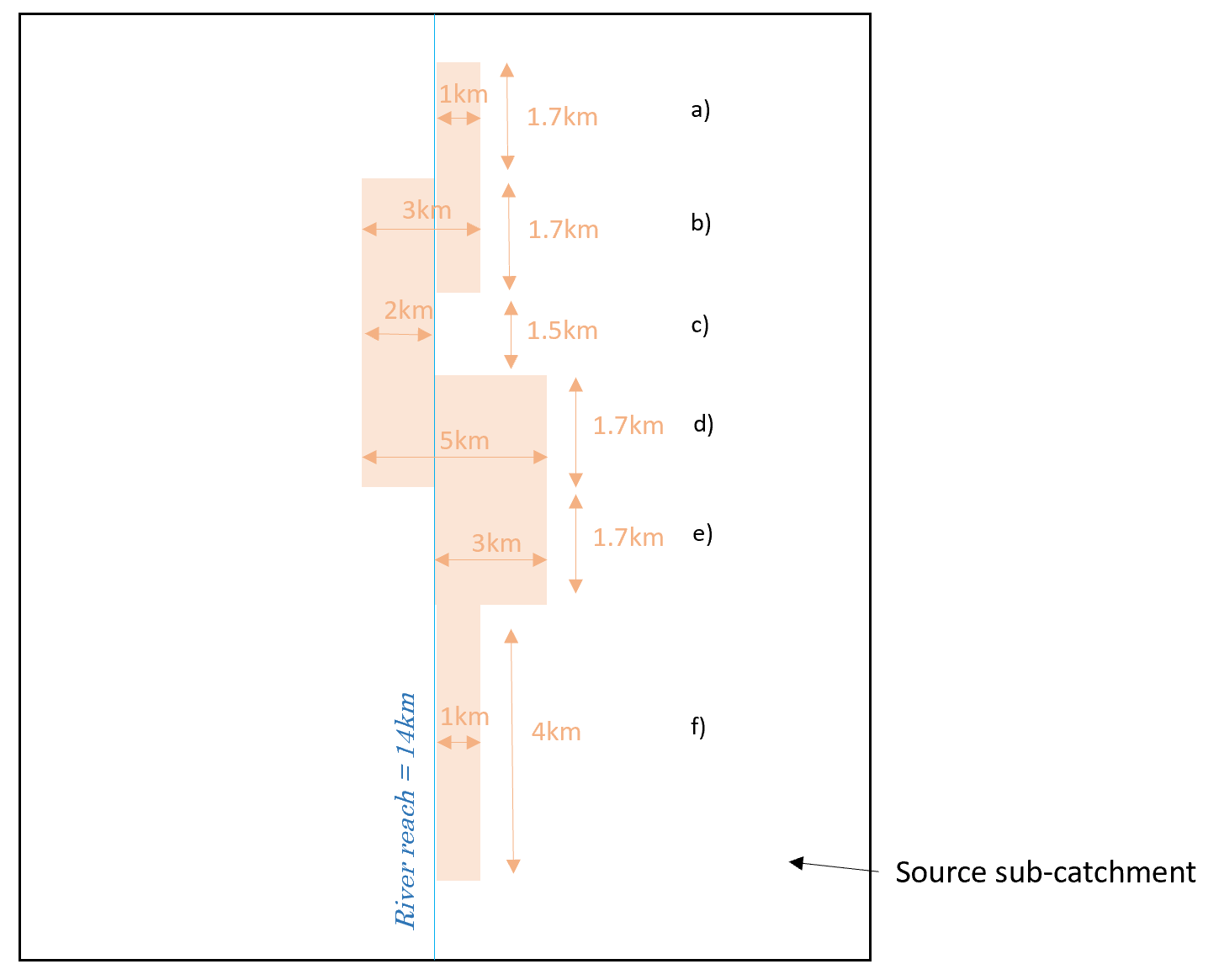
These inputs will require spatial data pre-processing - slopes can be extracted from the overlay of a Digital Elevation Model or a contour map and a land cover layer, and buffer widths and length percentages can be extracted from the overlay of a stream layer and a land cover layer. The RPM model provides for up to four buffer widths along a river reach. This requires that the width of riparian buffers along each link be re-classified into a maximum of four discrete classes. Buffer width is considered the total width on both sides of a river reach. The Hint below provides some background on how to derive the values for the buffer width and % length parameters.
Hint: Spatial pre-processing
In the example below only 3 buffer width classes are identified.
Buffer segment length (km) | Buffer segment average width (m) | Width class | Buffer width parameter | % of stream length | Buffer segment average slope (degrees) | |
|---|---|---|---|---|---|---|
| a) | 1.7 | 1 | buffer 1 <=2m | 2 | 12 | 5 |
| b) | 1.7 | 3 | buffer 2 2m-4m | 4 | 12 | 5 |
| c) | 1.5 | 2 | buffer 1 <=2m | 2 | 11 | 7 |
| d) | 1.7 | 5 | buffer 3 4m-6m | 6 | 12 | 2 |
| e) | 1.7 | 3 | buffer 2 2m-4m | 4 | 12 | 5 |
| f) | 4 | 1 | buffer 1 <=2m | 2 | 29 | 2 |
Parameters
Table 1. Model parameters
Parameter | Description | Units | Default | Range |
|---|---|---|---|---|
Adherence thickness | Average thickness of fine particles adhering to riparian vegetation | µm | 63 | 2 - 200 |
Stem radius | Average stem radius of riparian vegetation | m | 0.0005 | 0.0002 - 0.003 |
Surface bypass percentage | Percentage of surface runoff which bypasses riparian filtering processes | % | 30 | 0 - 100 |
Coarse particulate bulk density | In-situ bulk density of trapped coarse particulates | t/m3 | 1.5 | 0.5 - 2.5 |
Soil depth | Depth of unsaturated, porous surface soil layer present in the riparian zone | m | 0.2 | 0 - 1.0 |
Fine particulate bulk density | Bulk density of fine particulates adhered to riparian vegetation | t/m3 | 1.5 | 0.5 - 2.2 |
Initial effective vegetation height | Effective vegetation height at commencement of simulation run | m | 0.05 | 0 - 0.2 |
Lower damage threshold | Lower flow threshold at which damage to riparian vegetation begins to occur | m3/d/m | 500 | 0 - 5000 |
Maximum effective vegetation height | Maximum height of riparian vegetation where trapping of coarse particulates is possible | m | 0.05 | 0 - 0.2 |
Packing factor | Packing factor for fine particulates adhering to riparian vegetation | t/m3 | 0.524 | 0.3 - 0.6 |
Stem density | Stem density of riparian vegetation | stems/m2 | 1000 | 400 - 1600 |
Surface runoff percentage of quick flow | Surface runoff as a percentage of quick flow | % | 80 | 0 - 100 |
Total stream length | Total length of streams available for establishment of riparian buffers | m | Catchment specific | Catchment specific |
Upper damage threshold | Upper flow threshold at which riparian vegetation is totally damaged | m3/d/m | 3000 | 200 - 20,000 |
Daily vegetation growth rate | Daily growth rate of riparian vegetation | m/d | 0.001 | 0 - 0.005 |
Percentage of type 1 buffers | Percentage of type 1 buffers | % | 0 | 0 - 100 |
Slope of type 1 buffers | Mean slope of type 1 buffer areas | Degrees | 5 | 0 - 45 |
Width of type 1 buffers | Width of type 1 buffers | m | 0 | 1 - 50 |
Percentage of type 2 buffers | Percentage of type 2 buffers | % | 0 | 0 - 100 |
Slope of type 2 buffers | Mean slope of type 2 buffer areas | Degrees | 5 | 0 - 45 |
Width of type 2 buffers | Width of type 2 buffers | m | 0 | 1 - 50 |
Percentage of type 3 buffers | Percentage of type 3 buffers | % | 0 | 0 - 100 |
Slope of type 3 buffers | Mean slope of type 3 buffer areas | Degrees | 5 | 0 - 45 |
Width of type 3 buffers | Width of type 3 buffers | m | 0 | 1 - 50 |
Percentage of type 4 buffers | Percentage of type 4 buffers | % | 0 | 0 - 100 |
Slope of type 4 buffers | Mean slope of type 4 buffer areas | Degrees | 5 | 0 - 45 |
Width of type 4 buffers | Width of type 4 buffers | m | 0 | 1 - 50 |
Effective macroporosity | Quantity of soil macropores | m3/m3 | 0.2 | 0 - 1 |
Output data
The primary output from the model is a time series of particulate outputs from the riparian buffer following the simulation of riparian buffer processes. All outputs are provided at a daily time-step and are available to be routed through the Source stream network.
Reference list
Argent, R. M, Perraud, J-M, Podger, G. M, Murray, N (2008) WaterCAST Component Model Reference Manual, eWater CRC, Canberra.
Collier, K.J., A.B. Cooper, R.J. Davies-Colley, J.C. Rutherford, C.M. Smith, and R.B. Williamson. (1995) Managing riparian zones: a contribution to protecting New Zealand’s rivers and streams, Volume 2: Guidelines. Department of Conservation, Wellington, New Zealand.
Dillaha, T.A., R.B. Reneau, S. Mostaghimi and D. Lee. (1989) Vegetative filter strips for agricultural nonpoint source pollution control. American Society of Agricultural Engineers, 32(2): 513-519.
Flood, J.A. and N.J. Ashbolt. (2000) Virus-sized particles can be entrapped and concentrated one hundred fold within wetland biofilms, Advances in Environmental Research 3(4): 403-411.
Hairsine, P. (1997) Controlling sediment and nutrient movement within catchments. Cooperative Research Centre for Catchment Hydrology. Industry Report 97/9. http://www.catchment.crc.org.au/pdfs/industry199709.pdf
Hairsine, P.B., K. Bormann, and J. Brophy. (2001) Stock Tracks and the delivery of pollutants to streams by overland flow, In: I. Rutherford, F. Sheldon, G. Brierley and C. Kenyon. (eds), Third Australian Stream Management Conference, Brisbane, August 2001.
Hook, P.B. (2003) Sediment retention in rangeland riparian buffers. Journal of Environmental Quality, 32(3): 1130-1137.
Karssies, L.E. and I.P. Prosser. (1999) Guidelines for riparian filter strips for Queensland irrigators. Technical Report 32/99, CSIRO Land and Water, Canberra. Filters 45
Magette, W.L., R.B. Brinsfield, R.E. Palmer and J.D. Wood. (1989) Nutrient and sediment removal by vegetated filter strips. American Society of Agricultural Engineers, 32(2): 663-667.
McKergow, L.A., D.M. Weaver, I.P. Prosser, R.B. Grayson and A.Eg Reed. (2003) Before and after riparian management: particulate exports from a small agricultural catchment, Western Australia. Journal of Hydrology, 270: 253-272.
Mickelson, S.K., J.L. Baker and S.I. Ahmed. (2003) Vegetative filter strips for reducing atrazine and sediment runoff transport. Journal of Soil and Water Conservation, 58(6): 359-367.
Muñoz-Carpena, R., J.E. Parsons and J.W. Gilliam. (1999) Modelling hydrology and sediment transport in vegetative filter strips. Journal of Hydrology, 214: 111-129.
Newham, L., Rutherfurd, K. and Croke, B. (2005) A conceptual model of particulate trapping in riparian buffers. CSIRO Land and Water Technical Report http://www.clw.csiro.au/publications/technical2005/tr21-05.pdf
Parkyn, S. 2004. Review of riparian buffer zone effectiveness. Ministry of Agriculture and Forestry Technical Paper No: 2004/05, Wellington, New Zealand.
Rose C.W., W.L. Hogarth, H. Ghadiri, J-Y Parlange, A. Okom. (2002) Overland flow through a segment of uniform resistance. Journal of Hydrology 255(1-4): 134-150.
Rose, C. W., B. Yu, W. L. Hogarth, A. E. A. Okom and H. Ghadiri (2003) Sediment deposition from flow at low gradients into a buffer strip-a critical test of re-entrainment theory. Journal of Hydrology 280: 33-51.