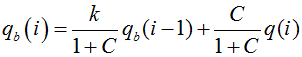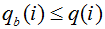Note: This is documentation for version 5.0 of Source. For a different version of Source, select the relevant space by using the Spaces menu in the toolbar above
Observed catchment runoff depth - SRG
An observed catchment runoff depth model allows the inclusion of an observed depth time series for rainfall-runoff and uses a digital filter to separate the quick flow and slow flow components.
Scale
An observed catchment runoff depth is applied to a functional unit (FU).
The model can be used at hourly to annual time-steps.
Principal developer
Cooperative Research Centre for Catchment Hydrology. The original slow flow filter was developed by Boughton (1993) and published as Method 2 in Grayson et al (1996, p78).
Scientific provenance
Chapman (1999) tested a number of base flow separation methods, with one, two and three parameters, and found that the formulation used here was the most satisfactory, while noting that fitting the parameters was subjective.
Version
Source v4.3
Dependencies
None.
Availability and conditions
The observed catchment runoff depth model is automatically installed with Source.
Structure and processes
Flow from functional units is required to be in two parts, quick flow and slow flow. When a time series of inputs is a source of runoff a method is required to separate this flow into these two components. The Observed Catchment Runoff Depth filter in Equation 1 identifies the base flow component of flow and when subtracted from the total flow gives the quick flow.
Equation 1 |
|---|
subject to
where:
qb(i) is filtered slow flow response for the ith sampling instant
q(i) is original stream flow for the ith sampling instant
k is the filter parameter given by the recession constant (several methods for computation given in Nathan and McMahon, 1990)
C is parameter that enables the shape of the separation to be altered (Grayson et al, 1996, p78)
It is applied as a single pass through the data.
Modifying the C and k parameters may be particularly useful when additional data are available on actual flow path separation eg tracer studies. See Chapman and Maxwell (1996). |
The equation may be used to fit a curve to the observed data by adjusting parameter C.
Table 1. Model parameters
| Parameter | Description | Default | Min | Max |
|---|---|---|---|---|
| k | Filter parameter given by the recession constant | 0.95 | 0 | 1 |
| C | Shape parameter | 0.15 | 0 | 1 |
The quick flow and slow flow should not be regarded as true amounts of surface (quick) and subsurface (slow) flow from the catchment. Only when additional information, such as from tracer studies, is available can physical interpretations be placed on the filtered responses (Grayson et al, 1996). |
Input data
The model requires daily stream flow data converted to a runoff depth across the catchment (e.g. in mm).
The time series needs to be continuous (free of gaps) and preferably with a long period (10+ years) of record. |
Selecting stream flow data to use in a river-basin scale simulation study needs information about the reliability of the data. It is best to use data which are most representative of the stream flow from the catchment. Observed data would normally be selected, except where the data are of poor quality or of unknown reliability. |
Parameters or settings
See Table 1, above (Values of k and C are provided for 13 Australian streams in Chapman, 1999).
Output data
The model outputs time series of quick flow and slow flow. Note that results are converted from depths to volumes before being output by multiplying by the catchment area.
References
Boughton, W. C. (1993) A hydrograph-based model for estimating the water yield of ungauged catchments. Hydrology and Water Resources Symposium: Towards the 21st Century: Newcastle: June 30 - July 2 1993: Preprints of Papers. pp 317-324.
Chapman, T. and Maxwell, A. (1996) Baseflow separation - comparison of numerical methods with tracer experiments 23rd Hydrology and Water Symposium: Water and the Environment. Preprints of Papers. 21-24 May 1996, Hobart, Tasmania, v.1, pp. 539-545.
Chapman, T. (1999) A comparison of algorithms for streamflow recession and baseflow separation. Hydrological Processes 13(5): 701-714.
Grayson, R.B., Argent, R.M., Nathan, R.J., McMahon, T.A. & Mein, R.G. (1996) Hydrological recipes: estimation techniques in Australian hydrology, Cooperative Research Centre for Catchment Hydrology, Clayton. pp. 77-79.
Nathan, R.J. & McMahan, T.A. (1990) Evaluation of automated techniques for baseflow and recession analysis. Water Resources Research, vol. 26, no. 7, pp. 1465-1473.